attention到底在做什么

机器学习

前言

近期看了anthropic的一些关于attention可解释性的文章，感觉很有意思，试着做了一些总结和思考，也希望给之后继续学习ml system层面对transformer的优化明确一些较为基本的常识，现记录在此。

回顾attention

attention数学形式

首先，我们先不要去考虑multi head和mask的事情（后文会慢慢引出），先从最为简单和朴素的attention开始，这样就会发现attention在数学上的表达是简单漂亮且有具体语义的，主要由四个部分组成，一个输入x(在不考虑batch_size的情况下，其维度为(sequence_length,d_model))，分别用于生成Q(query)、K(key)、V(value)的矩阵WqW_q、WkW_k、WvW_v，这些就是attention最为主要的几个变量了，Q与K负责attention的计算，其值代表着q位置对k位置信息的关注程度，V则代表着该位置所聚合的信息，基于这些变量，我们就得到了attention的计算公式：

Attenion(Q,K,V)=softmax(QKTdk)VAttenion(Q,K,V)=\mathcal{softmax}(\frac{QK^T}{\sqrt{d_k}})V

其中dkd_k就是query和key向量的维度，被广为认可的解释是为了防止点积过大带来的梯度计算问题，dkd_k只是一个常数，为了方便和美观，在后面的数学表达中忽略掉dkd_k。

我们将Q,K,V表达为分块向量的形式，也即

K=[k1k2⋮kT],Q=[q1q2⋮qT],V=[v1v2⋮vT]K = \begin{bmatrix} k_1 \\ k_2 \\ \vdots \\ k_T \end{bmatrix}, \quad Q = \begin{bmatrix} q_1 \\ q_2 \\ \vdots \\ q_T \end{bmatrix}, \quad V = \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_T \end{bmatrix}

其中ki,qik_i,q_i的维度是dkd_k,viv_i的维度是dvd_v,TT就是sequence的长度。

随后我们计算attention，得到

softmax(QKT)V=[q1⋅k1q1⋅k2⋯q1⋅kTq2⋅k1q2⋅k2⋯q2⋅kT⋮⋮⋱⋮qT⋅k1qT⋅k2⋯qT⋅kT][v1v2⋮vT]softmax(QK^T)V = \left[ \begin{array}{cccc} q_1 \cdot k_1 & q_1 \cdot k_2 & \cdots & q_1 \cdot k_T \\ q_2 \cdot k_1 & q_2 \cdot k_2 & \cdots & q_2 \cdot k_T \\ \vdots & \vdots & \ddots & \vdots \\ q_T \cdot k_1 & q_T \cdot k_2 & \cdots & q_T \cdot k_T \end{array} \right] \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_T \end{bmatrix}

这就是最朴素的attention结果，在实际使用中，尤其现在主流的大模型结构都已经是decoder-only结构的情况下，attention多为带mask的版本，所谓带mask的版本就是不允许前文中的token关注到后文中的token，其数学形式就是

softmax(QKT)V=[q1⋅k10⋯0q2⋅k1q2⋅k2⋯0⋮⋮⋱⋮qT⋅k1qT⋅k2⋯qT⋅kT][v1v2⋮vT]=[(q1⋅k1)v1(q2⋅k1)v1+(q2⋅k2)v2⋮(qT⋅k1)v1+⋯+(qT⋅kT)vT]\begin{align*} \text{softmax}(QK^T)V &= \left[ \begin{array}{cccc} q_1 \cdot k_1 & 0 & \cdots & 0 \\ q_2 \cdot k_1 & q_2 \cdot k_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ q_T \cdot k_1 & q_T \cdot k_2 & \cdots & q_T \cdot k_T \end{array} \right] \begin{bmatrix} v_1 \\ v_2 \\ \vdots \\ v_T \end{bmatrix} \\ &= \begin{bmatrix} (q_1 \cdot k_1)v_1 \\ (q_2 \cdot k_1)v_1 + (q_2 \cdot k_2)v_2 \\ \vdots \\ (q_T \cdot k_1)v_1 + \cdots + (q_T \cdot k_T)v_T \end{bmatrix} \end{align*}

KV cache
从带mask的attention得到的结果，我们可以解释为什么推理的时候需要kv cache，而q cache却并不被需要。
首先我们需要有一个概念，attention计算的结果是一个维度为(sequence_length,d_model)的向量，在做推理的时候，只会把最后一个维度的d_model向量用于计算最终的logits(用于计算词表中各个词的概率)，又结合推理过程是Next Token Prediction的形式，token是一个接着一个decode出来的，所以实际上只需要关注上文中带mask的attention计算结果最后一行的向量，可以看到这里会用到1到T所有的k和v，但是对于q则只会使用T位置的，故不存在q cache。
而对于训练，则会是每一个位置都会用于计算logits然后计算loss，且训练时全文可见，可以并行计算，不存在kv cache的问题。

multi heads

那么以上就是最为朴素的attention结构，也可以被称为一个head，那自然就会有multi heads的attention结构，它可以使得模型可以关注到更多层面的信息。首先输出x(维度为d_model)会被切割为若干个等长的vector，常见的有32、64等，然后每一个切割后的vector会由一个head计算，最终得到的所有vector会被直接concate在一起，并由一个WOW_O做一次线性变化作为输出，这就是multi head attention的结构。

有趣的数学建模

总述

attention结构被广泛应用在transformer架构中，我们的分析聚焦于现在主流的decoder-only的transformer结构，同时为了将关注点放在attention上并简化模型，我们忽略掉MLP，bias等。

我们先来建立一个感觉，从最简单的bigram词统计开始到其他更复杂的next token prediction的方法，对于下一个词的预测其实都可以理解为是对前文信息的汇总，bigram是容易理解的，它通过词统计来完成“训练”，然后根据距离待预测位置最近的一个token的信息来得到预测的token。

相对复杂的attention通过Q,K点乘得到的Attention矩阵来代表关注程度，V是sequence每个token位置所包含的信息,Attention矩阵与V相乘则是信息聚合的过程，信息聚合的结果就是attention的输出。

完全基于统计的bigram对于统计中从未出现过的新词往往无能为力，但基于attention的transformer却涌现出来一个比较有趣的能力——incontext learning能力，也即从未在训练数据中出现过的词，transformer仍然能够理解其含义并用于预测中，这体现出了基于attention的transformer信息聚合能力的强大。

几个数学建模

  • 残差流

    在transformer中，为了防止梯度消失，引入了残差的方法，将一个block的输出和其输入相加作为最终的输出。

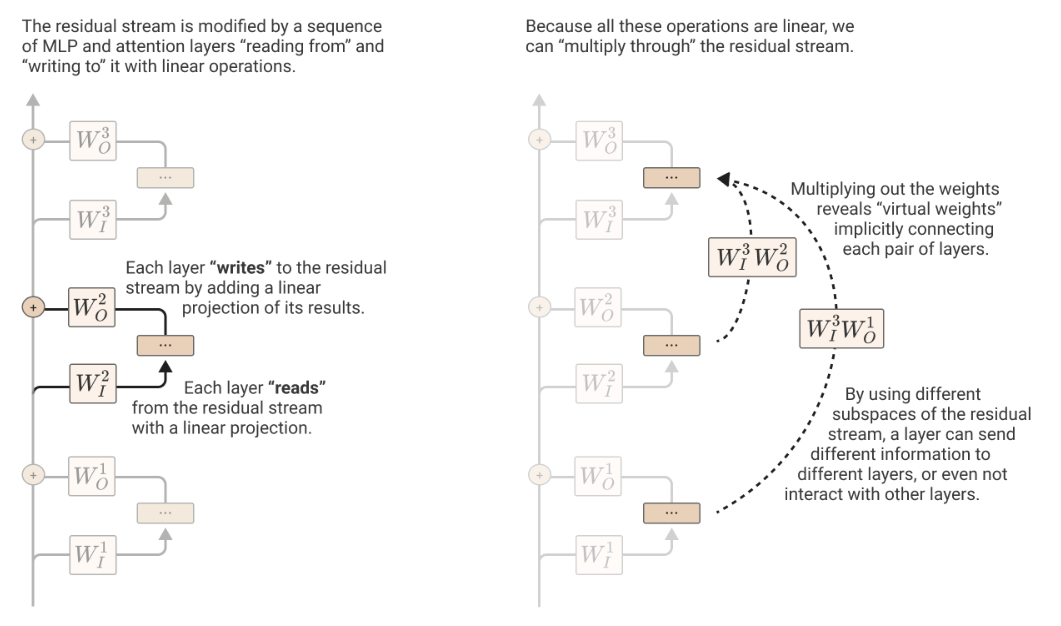
    alt text

    上图是一个multi head的示意图，我们主要分析左侧，每一个block会把上一个block的输出通过WIW_I线性变化，然后经过attention进行计算，最后通过WOW_O线性变化并进行残差操作作为输出。

    这里需要注意，由于需要进行直接的相加，所以必须保证输入和输出维度相同，也即最左侧的通道总是维度不变的向量，这就是残差流，维度大小蕴含着信息的压缩程度，可以理解为带宽。

  • 信息交换

    在残差流章节的图中是把一个sequence的所有token都放在一起的，实际上左侧的通道可以理解为是有token数条小通道捆绑在一起的，然后右侧block做的事情就是在这些独立的channel之间交流信息（因为线性变化可以跨矩阵列），这就是信息交流的过程。

    alt text

  • QK回路与OV回路

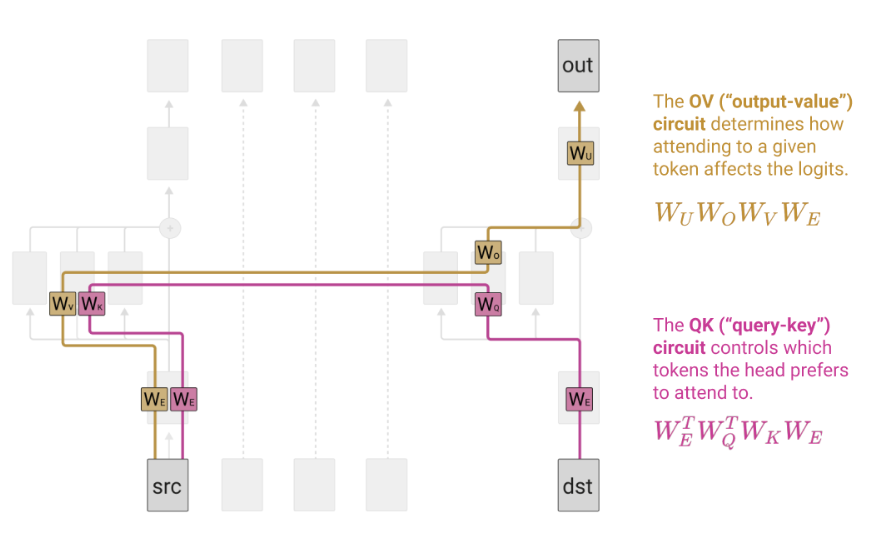
    QK回路和OV回路是对不同小通道之间信息交流的进一步细化的建模，下图中dst token即预测位置前一位的token，src为该token前任意一个token，首先二者通过QK回路计算出一个attention权重，该权重会与src token的embedding值相乘并通过src上的OV回路汇集到output中，通过这种建模我们可以把attention做的事情分为两个完全独立的步骤。

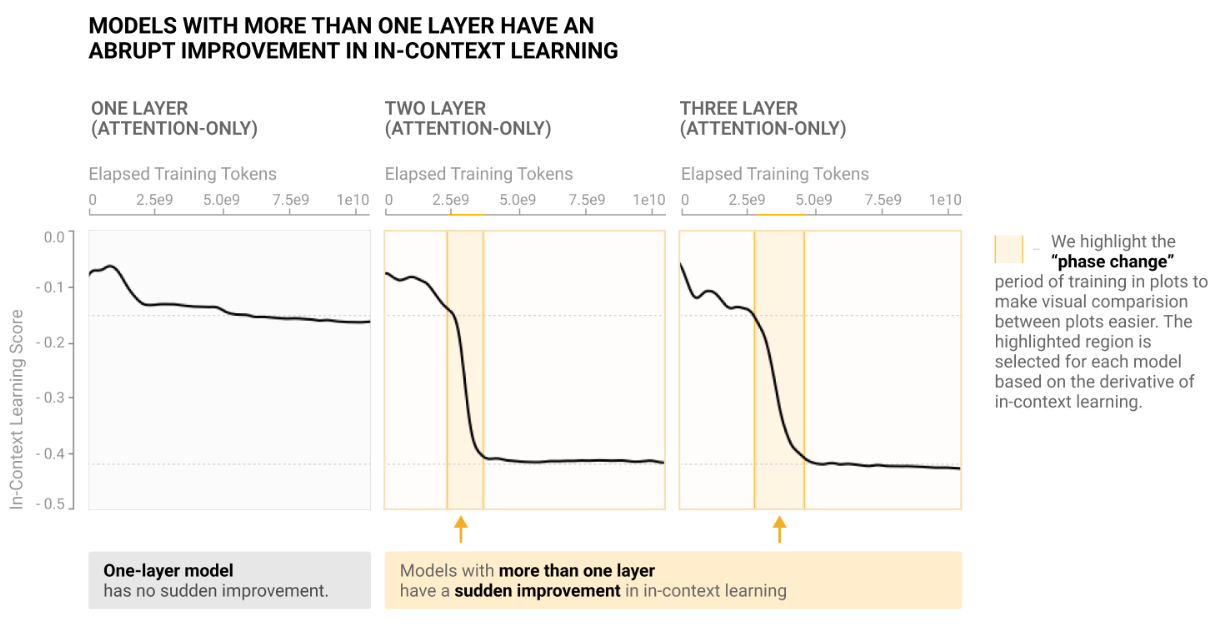
    alt text

incontext learning能力评测

incontext learning能力在两层以后开始涌现，关于利用上述建模对incontext learning的更多的分析可以参考"参考文献"板块的第二篇论文，该论文进行了丰富的实验来进行分析，在此就不放实验设计了。

alt text

参考文献

A Mathematical Framework for Transformer Circuits
https://transformer-circuits.pub/2021/framework/index.html

Incontext learning and induction heads
https://transformer-circuits.pub/2022/in-context-learning-and-induction-heads/index.html